[Leetcode]刷题记录帖

Posted on |
Words count in article: 3.9k | Reading time ≈ 16

Tree

题号分类

题目源地址

:one:基础:四种遍历的代码

T144先序遍历

1.迭代实现：(1) 利用栈 (2) 右孩子先进后出，左孩子后进先出->NLR

2.迭代代码的框架：特殊情况->一般情况

T94-中序遍历

1.递归实现：树的中序遍历实际上就是DFS

2.迭代代码:(1) 利用栈 (2) 尽量往左边遍历并且入栈 (3) 当左边遍历到NULL的时候再换到右边

T145-后序遍历

1.递归实现(iterative)

2.迭代代码(recursive)：较为复杂且太过经典,以后再看

T102-层序遍历

1.iterative实现：(1) 特殊情况 (2) 队列 (3) 一层一层遍历-当前队中的元素个数，结点出队，孩子结点入队

:two:PreOrder

T100平衡二叉树

1.recursive解法：根、左子树、右子树均符合isSameTree即可

1
2
3
4
if(p!=NULL && q!=NULL)
{
  return p->val == q->val && isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

2.递归边界-关键

1
return p==NULL && q==NULL;
T101对称二叉树

1.iterative解法：(1) 特殊情况 (2) 正常情况-特殊情况和正常情况的递归处理

1
2
3
4
5
6
//正常情况
if(left!=NULL && right!=NULL && left->val == right->val)
{
//镜像递归判断
return func(left->left,right->right) && func(left->right,right->left);
}
T226翻转二叉树

1.””翻转左右子树””的基本思想和””交换两个变量的值””类似

1
2
3
TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;

2.递归翻转左右子树

1
2
invertTree(root->left);
invertTree(root->right);

3.类似于PAT的A1102,但PAT里面的解法要稍微复杂一点

T257二叉树的所有路径

1.递归求解——二叉树的递归求解主要难点在根结点的处理，左右子树的处理一般递归处理即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//根是要根据题意处理，左右子树是递归处理
        bool isLeaf = root->left==NULL && root->right == NULL;
        if(isLeaf)
        {
            string p;
            for(auto it = path.begin();it!=path.end();it++)
            {
                p+=to_string(*it);//it是指针
                if(it!=path.end()-1) p+="->";
            }
            res.push_back(p);
        }
        if(root->left){btPath(root->left,path,res);}
        if(root->right){btPath(root->right,path,res);}
T112路径总和

1.递归方法：关键是实参

1
2
3
4
5
6
if(hasPathSum(root->left,sum - root->val) || hasPathSum(root->right,sum-root->val))
        {
            return true;
        }else
            return false;
				}

2.iterative解法：层序遍历，在遍历的过程中，将父节点的值累加到左右子结点上，当左右子结点的值等于目标值，则输出true；遍历结束还没有找到目标值的话输出false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//完全是在T102层序遍历的模板上修改的
bool hasPathSum(TreeNode* root, int sum) {
        queue<TreeNode*> q;
        //特殊情况处理
        if(root==NULL)
            return false;
        //
        q.push(root);
        TreeNode* tmp;
        while(!q.empty())
        {
            int size = q.size();
            while(size--)
            {
                tmp = q.front();
                q.pop();
                if(tmp->left!=NULL)
                {
                    q.push(tmp->left);
                    tmp->left->val+=tmp->val;
                }
                if(tmp->right!=NULL)
                {
                    q.push(tmp->right);
                    tmp->right->val+=tmp->val;
                }
                //叶子结点
                if(tmp->left==NULL && tmp->right==NULL && tmp->val==sum)
                {
                    return true;
                }
            }
        }
        return false;
        
    }
T113路径总和II

1.recursive解法：深度优先遍历，遍历一个结点则”目标值=目标值-当前遍历结点的值”，遍历至””当前节点的值等于目标值””则成功找到一条路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void dfs(TreeNode* root,int sum)
    {
        //边界
        if(root==NULL) return;
        //主体
        //成功找到
        if(root->val==sum && root->left == NULL && root->right == NULL)
        {
            path.push_back(root->val);
            res.push_back(path);
            path.pop_back();//清空path数组
            return;
        }
        //
        path.push_back(root->val);
        dfs(root->left,sum-root->val);//关键是递归函数的实参
        dfs(root->right,sum-root->val);
        path.pop_back();//为下条记录清空path
    }
T129求根到叶子节点数字之和

1.recursive解法：父节点的值*10累加到孩子结点的值上，累加所有的叶子结点的值,思想和方法上和T113类似

T298二叉树最长连续序列

1.要付费

T111二叉树的最小深度

1.recursive解法：叶子结点返回1；””有左子树没有右子树””或者””有右子树没有左子树””递归返回子树高度+1；””有左子树且有右子树””递归比较左右子树高度返回较小高度的值——关键是列出结点的所有情况：空、叶子、只有左或右子树、左右子树均有

####:three:postOrder

T104二叉树的最大深度

1.和T111完全一样，分五种情况递归

T110平衡二叉树判定

1.自己写出的通过测试的recursive解法:maxDepth()求树的高度，然后dfs递归遍历检查每个结点是否都符合BST的要求

2.柳神写出的通过测试的recursive解法：maxDepth()写法更简洁;把判断以每个节点为根的树是否为BST放在maxDepth()求解过程中，优化了效率。(柳神还是强:thumbsup:,自己还需要慢慢磨练

3.maxDepth()简洁写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//求maxDepth
int maxDepth(TreeNode* root)
    {
        if(root==NULL)
            return 0;
        int leftDepth,rightDepth;
        //
        if(root->left == NULL)
        {
            leftDepth = 0;
        }else
        {
            leftDepth = maxDepth(root->left);
        }
        if(root->right == NULL)
        {
            rightDepth = 0;
        }else
        {
            rightDepth = maxDepth(root->right);
        }
        //
        return (leftDepth>rightDepth? leftDepth : rightDepth)+1;
    }
T124二叉树中最大路径和

1.最大值只有四种情况：节点， 节点及左树，节点及右树，左右树及节点。最后一种情况不能作为左右树继续递归，需要保存临时最大值——关键是要知道只有这四种情况

T250 统计同值子树

1.付费题目

T366寻找完全二叉树的叶子节点

1.付费题目

T337打家劫舍 III

1.

BFS

T107二叉树的层次遍历 II

1.正常的层序遍历，不同之处在于””每层的结点值数组tmp””插入到res二维数组的头部——思想类似于：单链表头插法逆置

T103二叉树的锯齿形层次遍历

1.定义一个”isDouble”变量，单行则正常层序遍历，双行则头插法逆序遍历

注：这里因为是数组中的元素逆置，所以可以用stack或者数组头尾元素交换也可以

2.”!isDouble”不行，得用”isDouble = !isDouble”,来将isDouble取反

T199二叉树的右视图

1.正常层序遍历，然后在将每层数组的最后一个元素插入到res的一维数组中，然后输出res即可

2.这里找””每层数组的最后一个元素””有个小技巧

1
2
//每层遍历之后，tmp指向的是当层的最后一个元素
res.push_back(tmp->val);

BST:Binary Search Tree:左<根<右

T98验证二叉搜索树

1.柳神的思路：BST中序遍历的结果是递增数组——这是BST的一个重要性质！！！

注意：特殊情况的判定有两种情况

1
2
3
//第二种情况的判定”保证数组中至少有两个元素“
if(root==NULL || (root->left == NULL && root->right == NULL))
  return true;

2.自己第一次尝试的错误思路：分四种情况递归处理-左右孩子都没有、左右孩子都有、有左孩子没有右孩子、没有左孩子有右孩子——这种思路只能保证结点符合，但不能保证整棵树符合BST

1
[10,5,15,null,null,6,20]
T235二叉搜索树的最近公共祖先

1.分为五种情况,递归处理——主要是五种情况都要考虑周全,不能遗漏任何一种情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
if(root->val == p->val)
				{
            return p;
        }
        if(root->val == q->val)
        {
            return q;
        }
        if(root->val > p->val && root->val > q->val)//左子树
        {
            return lowestCommonAncestor(root->left,p,q);
        }
        if(root->val < p->val && root->val < q->val)//右子树
        {
            return lowestCommonAncestor(root->right,p,q);
        }
        // if((root->val > p->val && root->val < q->val) || (root->val < p->val && root->val > q->val))
        // {
        //     return root;
        // }
        return root;

2.LC题解简单版本：这里没有用到BST的特性来判断p、q是否在左右子树，而是以*递归返回值是否是NULL来判断结点p、q是在左子树还是右子树，所以这种解法适用于普通的二叉树，也就是T236

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
if(root==NULL)
            return NULL;
	//合二为一
        if(root==p || root==q) return root;
//关键
        TreeNode* left = lowestCommonAncestor(root->left,p,q);
        TreeNode* right = lowestCommonAncestor(root->right,p,q);
//剩下三种情况
        if(left!=NULL && right !=NULL)
            return root;
        else if(left != NULL)//说明right==NULL，即p、q均不在右子树
            return left;
        else if(right != NULL)
            return right;
        return NULL;
T236二叉树的最近公共祖先

1.解法和T235的LC解法版本一致

T108将有序数组转换为平衡二叉树

1.柳神解法：将区间[left,right]中的mid=(left+right)/2作为根节点，左边递归构建左子树，右边递归构建右子树——考研初试可能会考，背下来！

1
2
3
4
5
6
7
8
9
10
11
12
13
//数组，左，右
    TreeNode* func(vector<int>& nums,int left,int right)
    {
        //
        if(left>right)
            return NULL;
        //
        int mid = (left+right)/2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = func(nums,left,mid-1);
        root->right = func(nums,mid+1,right);
        return root;
    }
T109有序链表转换二叉搜索树

1.思路同T108，只是在有序链表中找中点，也就是根节点的值的方法要用到快慢指针——T108和T109的特殊之处在于都为升序,这给递归处理提供了条件

2.这里的函数的参数和T108中的参数的含义有所不同，

1
2
3
4
5
6
7
8
9
//T108
//right表示的当前区间的[left,right]中的right
TreeNode* func(vector<int>& nums,int left,int right)
func(nums,0,nums.size()-1);
//T109
//tail表示的是当前链表的尾结点的下一个结点
TreeNode* func(ListNode* head,ListNode* tail)
//所以调用函数的初值为
func(root,NULL);
T173二叉搜索树迭代器-next()返回最小元素

1.利用二叉搜索树的中序遍历序列是递增的性质。

T230二叉搜索树中第K小的元素

1.利用二叉搜索树的中序遍历序列是递增的性质——最普通

2.优化：找到第k个数的时候就返回

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//TreeNode和k为输入参数，res是用于返回的参数-
void inOrder(TreeNode* root,int &k,int &res)
    {
        if(root==NULL)
            return;
        //
        if(root->left)
        {
            inOrder(root->left,k,res);
        }
        k--;//因为左边是小的数，遍历一个左边的数就k--
        if(k==0)
        {
            res = root->val;//通过”&res“返回参数
            return;
        }
        if(root->right)
        {
            inOrder(root->right,k,res);
        }
    }
T297二叉树的序列化与反序列化

1.LC有关树的题中，树的序列化与反序列化就是这题

T285

1.付费题

T270

1.付费题

T272

1.付费题

T99恢复二叉搜索树

1.Hard-待刷

重要程度

T156很少考

1.付费题

T114很少考二叉树展开为链表

[注]in-place 原地

1.本题理解题意很关键：其实就是返回二叉树先序遍历结果的链表形式—树中结点有左右孩子，而链表中结点左孩子为NULL，右孩子为先序遍历的下一个结点

2.细节处理要注意：最后一个结点不用处理，所以循环的终点是”res.size()-1”

1
2
3
4
5
6
7
//将res中的元素串成链表
//最后一个结点不用设置左右孩子分别为NULL，因为最后一个结点在最后一层
        for(int i=0;i<res.size()-1;i++)//最后一个元素不用设置左右孩子结点
        {
            res[i]->right = res[i+1];//这里不能用i++,否则i会自增
            res[i]->left = NULL;
        }
T255很少考验证前序遍历序列二叉搜索树

1.付费

T333很少考最大 BST 子树

1.付费

T222很少考完全二叉树的节点个数

[注]complete binary tree 完全二叉树

1.自己想的思路：层序遍历找出第一个没有同时有左右孩子的结点并且记录此结点的在二叉树中的序号，如果是没有左孩子，则return numX2-1;如果没有右孩子，则return numX2;

2.柳神的解法：完全二叉树满足当最左结点和最右结点等高时，结点个数为2^h-1，否则等于””左子树的结点数+右子树的结点数+1“，左右子树可以递归处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int countNodes(TreeNode* root) {
        if(root==NULL)
            return 0;
        //
        TreeNode *l = root,*r = root;
        int cntLeft = 0,cntRight = 0;
        while(l != NULL)
        {
            l = l->left;
            cntLeft++;
        }
        while(r != NULL)
        {
            r = r->right;
            cntRight++;
        }
        if(cntLeft==cntRight) return pow(2,cntLeft)-1;
  //关键：左右子树递归处理
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
T105很少考从前序与中序遍历序列构造二叉树

1.在PAT中训练过，但是有个细节：构建root结点的代码，在PAT和LC中分别犯了不同的错误

1
2
//PAT中的错误是申明的不是结点的指针；LC中的错误是没有用new语句
TreeNode* root = new TreeNode(pre[preL]);
T106很少考从中序与后序遍历序列构造二叉树

1.思路同PAT中的题目，但是有一个小的细节经常出错：

1
2
//遍历in数组找出根节点在in数组中的位置，now的初始值是inL，不是0，经常错！
int now = inL;//经常出错！
T116重要填充每个节点的下一个右侧节点指针

[注]perfect binary tree 完美二叉树(即满二叉树);populate填充，population人口

1.自己想的正确的解法(空间复杂度不满足o(1))：层序遍历，每层遍历的时候判断size的值确定next为下一个结点还是NULL。注意这里有个细节

1
2
3
//这里在”()“里面的话，size的值没有减1；但是一旦出了”()"",size就减一了；并不是出了”"{}"之后size才减一
while(size--)
{}

2.网友的递归解法：分两种情况-根结点为root，对于左孩子，next指向右孩子；对于右孩子，指向root->next的左孩子(背下来)

1
2
3
4
5
6
7
8
9
10
11
12
void func(Node* root,Node* right_r)
    {
  //设置root->next
        root->next = right_r;
        //
        if(root->left)
        {
          //两种情况
            func(root->left,root->right);
            func(root->right,right_r?right_r->left:NULL);
        }
    }
T117重要

1.层序遍历可以解决，空间复杂度不是o(1)

2.递归解法-中文版精选评论有递归解法，稍微有点麻烦，但必须掌握！

T314重要二叉树的垂直遍历

1.付费题

T96重要不同的二叉搜索树——卡特兰数

卡特兰数详解

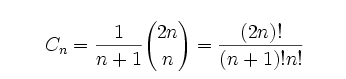
1.二叉搜索树的中序遍历固定，以栈的角度理解，中序遍历就是出栈的顺序，先序遍历就是入栈的顺序，而先序遍历和中序遍历就能唯一确定一棵树->转化为出栈顺序固定，入栈顺序有多少种？公式法

2.卡特兰数的解题模板：动态规划

T95很少考不同的二叉搜索树 II——输出所有的BST

1.动态规划

T331很少考验证二叉树的前序序列化

1.实际上是验证是否为完全二叉树，且给出的序列是先序遍历，所以可以用元素入栈来模拟先序遍历->从下往上看，出现两个空节点则消除一个正常结点，最后只留下根节点为空节点

Graph

题号分类

题目源地址

基础

T133
T399
T310

###图形学

T133
T133
T335
T356
T391
T223